Sensitivitätsanalyse

Aus Controlling-Wiki
Geprüft: Positiv beurteilt

Die Sensitivitätsanalyse, auch Empfindlichkeitsanalyse genannt, ist ein Verfahren, welches Unternehmen helfen soll, die kritischen Werte und den Einfluss einzelner Risiken auf ökonomische Zielgrössen zu untersuchen. Sie wird verbreitet im Investitionscontrolling und in der Investitionsrechnung angewendet. Mit der Sensitivitätsanalyse wird der Einfluss von Veränderungen der Eingangsdaten auf die Zielgrösse aufgezeigt, wie z. B. der Nutzungsdauer einer Investition auf dessen Kapitalwert (Fischer, Möller & Schultze, 2015, S. 513-514; Hölscher & Helms, 2018, S. 142; Wöhe & Döring, 2013, S. 58-59). Damit beruht die Sensitivitätsanalyse auf der Annahme, dass die Werte der Inputgrössen um einen geschätzten Wert schwanken können (Wöhe & Döring, 2013, S. 511). Von Interesse sind die Auswirkungen z. B. auf den Gewinn bei Veränderung einer oder mehrerer Inputvariablen wie bspw. Preis, variable Stückkosten, Fixkosten oder Absatzmenge (Gladen, 2014, S. 58-59).

Zweck

Die Sensitivität zeigt die Empfindlichkeit des Output-Wertes bei der Variation eines bestimmten Input-Wertes an (Taschner, 2017, S. 122). Nach Taschner (2017) gilt es folgende Frage zu beantworten: «Wie stark ändert sich das Ergebnis, wenn der zu untersuchende Inputfaktor systematisch innerhalb eines bestimmten Werteintervalls variiert wird bzw. eine Reihe von definierten Alternativwerten annimmt?» (S. 122). Die Sensitivitätsanalyse verfolgt zwei verschiedene Zwecke. Auf der einen Seite soll durch sie die Unsicherheit im Umgang mit dem aufgestellten Modell reduziert werden. Auf der anderen Seite leistet sie einen Beitrag zur Steuerung von praktischen Massnahmen. Wirkt ein Faktor besonders sensibel auf die Zielgrösse des Modells, können zur Unterstützung Massnahmen ergriffen werden, die den ökonomischen Effekt maximieren. Wirken sich allerdings mehrere verschiedene Variablen oder Variablenkombinationen besonders stark auf die Zielgrösse aus, so kann der grösste ökonomische Nutzen durch die Auswahl des effizientesten Weges erzielt werden (Preuss, 2011, S. 169).

Anwendungsbereiche

Grundsätzlich ist die Sensitivitätsanalyse auf jedes mathematische Modell anwendbar (Preuss, 2011, S. 169). Sensitivitätsanalysen sind geeignet, wenn zwischen den Risikoparametern und der gewünschten Zielgrösse eine funktionale Beziehung besteht, welche mit einer mathematischen Gleichung beschrieben werden kann (Fischer et al., 2015, S. 519). Da Planwerte Zukunftswerte sind, muss davon ausgegangen werden, dass sie die zukünftige Realität nicht vollständig abbilden können. Es ist daher ratsam, zuerst mit den wahrscheinlichsten Daten zu rechnen und anschliessend eine Sensitivitätsanalyse durchzuführen (Varnholt, Lebefromm & Hoberg, 2012, S. 539). Mit dieser können nach Wöhe und Döring (2013) die folgenden zwei Fragen beantwortet werden (S. 504):

  • Welche Risikofaktoren haben einen besonders grossen Einfluss auf die Zielgrösse?
  • In welchem Bereich können sich die Risikofaktoren bewegen, ohne dass sich die Vorteilhaftigkeit eines Projektes ändert?

Die Werte der Risikofaktoren, welche einen grossen Einfluss auf das Ergebnis haben, werden als kritische Werte bezeichnet. Sie signalisieren die Grenze, bei der sich die Vorteilhaftigkeit verändert, wenn beispielsweise ein Kapitalwert negativ oder eine alternative Mittelverwendung rentabler wird. Durch ihre Eigenschaften erweist sich die Sensitivitätsanalyse vor allem im Bereich der Investitionsrechnung als geeignetes Instrument. Sie liefert jedoch keine Hinweise darauf, welche Investitionsalternative zu bevorzugen ist, sondern zeigt lediglich den Einfluss spezifischer Risikofaktoren auf die Zielgrösse (Wöhe & Döring, 2013, S. 504-505).

Verfahren

Die Vorgehensweise beim Verfahren der kritischen Werte ist wie folgt (Müller, 2014, S. 482-483):

  1. Kriterium der Vorteilhaftigkeit bestimmen sowie die unsicheren Inputgrössen ermitteln
  2. Bestimmungsgleichung für die Ermittlung der Vorteilhaftigkeit aufstellen
  3. Gleichung nach gewünschter Variablen auflösen

Weiteres zur Vorgehensweise beim Verfahren der kritischen Werte wird auf der Seite Investitionsrechnung unter dynamischer Amortisationsvergleich und Kostenvergleich erläutert. Die zweite Variante der Sensitivitätsanalyse bedient sich einer Gleichung, bei der in der Regel eine Variable beliebig oft um einen bestimmten Prozentsatz verändert wird. Diese Reaktionen, auch Sensitivitäten genannt, der Zielgrösse auf die sich ändernden Variablen werden in Prozent angegeben und bilden die Basis der Untersuchung (Fischer et al., 2015, S. 513-514; Müller, 2014, S. 483). Zur Veranschaulichung folgt ein Beispiel einer Investitionsrechnung:

Die Schreinerei Muster AG überlegt sich neu auch Stühle zu produzieren und über bestehende Kanäle abzusetzen. Für die Aufnahme der Produktion muss eine neue Maschine im Wert von CHF 400‘000 angeschafft werden. Die Lebensdauer der Maschine beträgt fünf Jahre. Die Herstellkosten pro Stuhl betragen CHF 150. Der Geschäftsführer Peter Muster rechnet damit, jährlich 1‘000 Einheiten zu einem Preis von CHF 250 absetzen zu können.

Jahr 0 Jahr 1 Jahr 2 Jahr 3 Jahr 4 Jahr 5 Total
Investition -400'000 0 0 0 0 0 -400'000
Absatzmenge 1'000 1'000 1'000 1'000 1'000
Verkaufspreis 250 250 250 250 250
Herstellkosten 150 150 150 150 150
Deckungsbeitrag 100'000 100'000 100'000 100'000 100'000 500'000
Überschuss 100'000

Sofern die Annahmen von Peter Muster stimmen, lohnt sich die Aufnahme der Produktion von Stühlen. Doch wie sieht es aus, wenn die effektiven Absatzmengen und Preise nicht den geplanten Werten entsprechen? Mit einer Sensitivitätsanalyse können die Risiken der Abweichungen aufgezeigt werden.

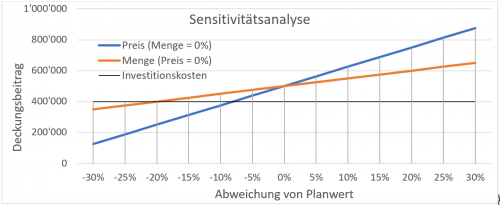
Abb. 1: Die Sensitivitätsanalyse am Beispiel der Schreinerei Muster AG

Die in Abbildung 1 ersichtliche Sensitivitätsanalyse zeigt auf, dass die Deckungsbeiträge beim Preis stärker variieren als bei der Menge. Der kritische Wert für den Preis liegt ceteris paribus acht Prozent unter dem Planwert. Kann Peter Muster nicht jährlich 1‘000 Stühle zu einem Preis von CHF 230 (250*0.92) verkaufen, wird die Stuhlproduktion zu einem Verlustgeschäft. Die Absatzmenge ist weniger sensitiv. Der kritische Wert liegt dort bei -20%, was 800 Stühlen (1000*0.8) entspricht. Dieses Beispiel ist sehr einfach konzipiert, die Sensitivitätsanalyse eignet sich jedoch auch für komplexe Fragestellungen (Buchhart & Burger, 2002, S. 110-111)

Erweiterungen

Die Sensitivitätsanalyse kann durch eine Risikoabschätzung und/oder eine Monte-Carlo-Simulation erweitert werden.

Risikoabschätzung

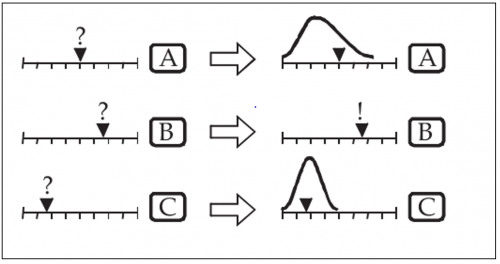
Nach Taschner (2017) beschäftigt sich die Risikoabschätzung mit folgenden Fragen: «Wie wahrscheinlich ist es, dass die als kritisch identifizierten Inputfaktoren bestimmte Werte annehmen? Wie hoch ist das Risiko, dass sich andere Werte als die ursprünglich angenommen[en] Basiswerte ergeben?» (S. 128). Somit müssen mögliche Wertebereiche (Minimum, Maximum und Wahrscheinlichkeitsverteilung) für die kritischen Inputfaktoren ermittelt werden. In Abbildung 2 sind auf der linken Seite die drei Inputfaktoren mit dem jeweiligen Schätzungswert ersichtlich. «Input B» ist ein nicht-kritischer Inputfaktor, so wird dieser Wert beim Schätzungswert fixiert. Für die beiden kritischen Inputfaktoren werden nun mögliche Wertebereiche ermittelt. Dies wird vom Erstellenden «nach bestem Wissen und Gewissen» gemacht. Dazu können auch passende Verteilungen wie die Dreiecksverteilung, Gleichverteilung, Normalverteilung sowie weitere Verteilungen zur Hilfe genommen werden. Dabei sollte das Aufwand-Ertrag-Verhältnis berücksichtigt werden. Es ist zu beachten, dass die gewählten Minimum- und Maximumwerte ausschlaggebender sind als die Form der Verteilung. Aus diesem Grund sollte der Aufwand für die Bestimmung der Wahrscheinlichkeitsverteilung nicht zu hoch ausfallen. Für die beiden kritischen Inputwerte wurde die Normalverteilung angewendet, wobei es sich bei «Input C» um eine steilere Normalverteilung (kleinerer Wertebereich) handelt als bei «Input A».

Abb. 2: Wahrscheinlichkeitstransformation von Inputvariablen (Taschner, 2017, S. 129)

Monte-Carlo-Simulation

Bei der Monte-Carlo-Simulation handelt es sich um eine mathematische, computerunterstützte Technik, mit der das Risiko in quantitativer Analyse und Entscheidungsfindung nachgewiesen werden kann (Palisade, online). Sie kommt im wirtschaftlichen Kontext vor allem zum Einsatz, wenn es darum geht, die Unsicherheit noch präziser zu analysieren (Varnholt et al., 2012, S. 540). In diesem Beispiel stellt sich nach Taschner (2017) bei der Monte-Carlo-Simulation folgende Frage: «Mit welcher Wahrscheinlichkeit wird der Output des Business Case bestimmte Werte annehmen, wenn die Inputfaktoren die ermittelten Wahrscheinlichkeitsverteilungen aufweisen?» (S. 129). Um die Antwort auf die Frage zu erhalten, wird der Business Case mehrmals mit verschiedenen Inputkombinationen aus Zufallszahlen der einzelnen Wahrscheinlichkeitsverteilungen durchgerechnet. Dabei wird der «Output X» immer festgehalten. Mithilfe von kommerziellen Softwareprogrammen oder Excel Add-ins lässt sich die Monte-Carlo-Simulation zeitnah, ohne grossen Aufwand und sehr bequem durchführen. Dabei leisten die Tools Hilfe, indem sie den anwendenden Personen ermöglichen, für die jeweiligen kritischen Inputfaktoren eine Wahrscheinlichkeitsverteilung zu hinterlegen, mit der die weiteren Berechnungen erfolgen.

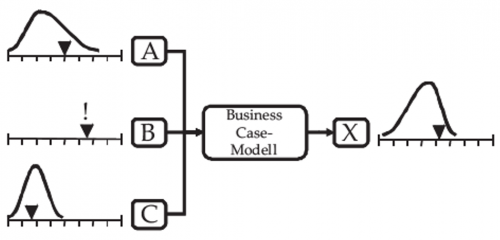
Abb. 3: Simulationsergebnis (Taschner, 2017, S. 130)

Per Knopfdruck werden dann mehrere hundert oder tausend Szenarien mit den verschiedenen Inputkombinationen aus Zufallszahlen, die innerhalb der Wahrscheinlichkeitsverteilungen liegen, durchgerechnet. Da jeweils die unterschiedlichen «Outputs X» festgehalten werden, ergibt sich aus den «Outputs X» wiederum eine Wahrscheinlichkeitsverteilung, was in Abbildung 3 ersichtlich ist (Taschner, 2017, S. 129-130). Somit resultieren aus der Monte-Carlo-Simulation eine Wahrscheinlichkeitsverteilung für den «Output X» mit Minimum-, Maximum- und Erwartungswert sowie weitere mathematische Grössen.

Vor- und Nachteile

Im Folgenden sollen einige zentrale Vor- und Nachteile der Sensitivitätsanalyse aufgeführt werden.

Vorteile Nachteile
Die Abhängigkeit des Investitionserfolgs von den kritischen Faktoren wird deutlich und somit auch das Risiko einer Investition. Die Entscheidungsverantwortlichen erfahren, für welche Faktoren sie weitere Informationen beschaffen und auswerten sollten (Bösch, 2016, S. 332). Es wird immer nur ein kritischer Faktor angeschaut. Wechselwirkungen zwischen den Inputgrössen werden dabei nicht berücksichtigt. Wenn der Erfolg einer Investition von mehreren Faktoren abhängt, nimmt die Aussagekraft der Sensitivitätsanalyse ab (Prokop, 2008, S. 468).
Der Rechenaufwand bei der Sensitivitätsanalyse ist gering und das Vorgehen leicht verständlich für Dritte (Prokop, 2008, S. 468). Es kann nicht objektiv geklärt werden, ob die Ergebnisse für die Investition eine grosse Rolle spielen oder nicht (Prokop, 2008, S. 468).
Die Unsicherheiten im Umgang mit dem gewählten Modell können reduziert und die Steuerung von praktischen Massnahmen verbessert werden (Preuss, 2011, S. 169). Mögliche weitere Einflussfaktoren wie beispielsweise die Konjunkturentwicklung, Reaktionen der Konkurrenz oder technologische Veränderungen werden ausser Acht gelassen (Bösch, 2016, S. 332).
Es können mögliche Zusammenhänge zwischen den Inputgrössen aufgedeckt und analysiert werden (Müller, 2014, S. 483). Sie liefert keine Informationen zu Gründen und Ursachen für Abweichungen der kritischen Werte zu den Schätzwerten. Auch die Eintrittswahrscheinlichkeit von Abweichungen wird durch dieses Verfahren nicht bekannt (Bösch, 2016, S. 332).

Kritische Würdigung

Die Sensitivitätsanalyse ist ein geeignetes Instrument, um spezifische Veränderungen von Variablen und deren Auswirkung auf das Gesamtergebnis zu ermitteln. Darüber hinaus gibt das Verfahren Auskunft, welche Inputgrössen einen besonders starken Einfluss auf den Output haben und somit eine starke Bedeutung haben. Zudem verursacht die Analyse nur einen relativ geringen Aufwand (Hölscher & Helms, 2018, S. 145).

Weniger vorteilhaft ist jedoch, dass das Verfahren keine Entscheidungsregeln hat und somit die Problematik der Investitionsentscheidung nicht lösen kann. Ausserdem ist die Ceteris-paribus-Bedingung problematisch, da dadurch die Eingabegrössen als unabhängig voneinander betrachtet werden. In der Realität trifft dies nicht zu, da sich die Parameter untereinander durchaus beeinflussen können. Ausserdem berücksichtigt die Sensitivitätsanalyse die Eintrittswahrscheinlichkeit der Veränderungen nicht. So dient das Verfahren eher einer groben Abschätzung von Unsicherheiten (Fischer et al., 2015, S. 514; Hölscher & Helms, 2018, S. 145; Müller, 2014, S. 483). In der Monte-Carlo-Simulation werden in der Berechnung die Wahrscheinlichkeiten berücksichtigt, was sie wesentlich aussagekräftiger als die Sensitivitätsanalyse macht. Eine Monte-Carlo-Simulation ist jedoch äusserst aufwendig und setzt fundierte mathematische Kenntnisse voraus (siehe Risikocontrolling) (Sartor & Bourauel, 2013, S. 76-81).

Lern- und Praxismaterialien

Aufgaben

Quellen

Autoren

Fabrizio Russi, Matteo Salis, Ardi Sopi, Tobias Stierli, Lukas Wallimann

Abgerufen von „https://wiki.hslu.ch/controlling/index.php?title=Sensitivitätsanalyse&oldid=15187“