Monte-Carlo-Simulation: Unterschied zwischen den Versionen
| Zeile 7: | Zeile 7: | ||
Die Monte-Carlo-Simulation, welche ihren Ursprung in den stochastischen und statistischen Methoden hat, verfolgt das primäre Ziel der experimentellen Ermittlung von Wahrscheinlichkeitsverteilungen bei Zufallsgrössen. Dabei können, basierend auf den Risikofaktoren und deren Wahrscheinlichkeitsverteilungen, unbekannte Strukturen und Verhalten simuliert werden (Sartor & Bourauel, 2013, S. 76). Damit eine plausible und praxisnahe Einschätzung des Gesamtrisikoumfangs vorgenommen werden kann, werden bei der Monte-Carlo-Simulation mehrere zukünftig mögliche Risikoszenarien kalkuliert sowie analysiert (Gleißner, 2017, S. 254). | Die Monte-Carlo-Simulation, welche ihren Ursprung in den stochastischen und statistischen Methoden hat, verfolgt das primäre Ziel der experimentellen Ermittlung von Wahrscheinlichkeitsverteilungen bei Zufallsgrössen. Dabei können, basierend auf den Risikofaktoren und deren Wahrscheinlichkeitsverteilungen, unbekannte Strukturen und Verhalten simuliert werden (Sartor & Bourauel, 2013, S. 76). Damit eine plausible und praxisnahe Einschätzung des Gesamtrisikoumfangs vorgenommen werden kann, werden bei der Monte-Carlo-Simulation mehrere zukünftig mögliche Risikoszenarien kalkuliert sowie analysiert (Gleißner, 2017, S. 254). | ||
{| | {| | ||
|- valign="bottom" | |- valign="bottom" | ||
|style="width:100%"| | |style="width:100%"| | ||
== Monte-Carlo-Simulation am Beispiel der Unternehmensplanung (Anwendungsgebiete) == | == Monte-Carlo-Simulation am Beispiel der Unternehmensplanung (Anwendungsgebiete) == | ||
|align="right"|[[Datei:Flag_für_Strategie.png|link=Strategie|Strategie]] | |align="right"|[[Datei:Flag_für_Strategie.png|link=Strategie|Strategie]] | ||
Version vom 13. Oktober 2021, 09:54 Uhr
Die Monte-Carlo-Simulation ist ein Begriff aus der Stochastik und stellt ein Verfahren dar, welches zur Analyse und Beurteilung von Risiken im Risikocontrolling verwendet wird (Sartor & Bourauel, 2013, S. 77). Mithilfe dieser computerbasierten Simulationsmethode können Wahrscheinlichkeiten berechnet werden. Die Idee darin besteht, ein Experiment viele Male zu simulieren und mithilfe des Gesetzes der grossen Zahl eine Wahrscheinlichkeit zu ermitteln (Kroese et al., 2014, S. 386). Daraus entsteht eine repräsentative Anzahl möglicher Zukunftsszenarien (Gleißner & Wolfrum, 2019, S. 51). Die heute verfügbare Rechenleistung ermöglicht es, nahezu beliebig komplexe Planungsmodelle zu simulieren (Gleißner & Wolfrum, 2019, S. 25). Ihr Einsatzgebiet ist hauptsächlich im Bereich Risikomanagement, sie findet jedoch auch ihre Anwendung in anderen Gebieten wie der allgemeinen Unternehmensplanung (Grisar & Meyer, 2015, S. 262).
Begriffsdefinition
Im Fürstentum Monaco gibt es einen Stadtteil Monte-Carlo, in welchem sich die weltbekannte Spielbank Monte-Carlo befindet (Hager, 2004, S. 145). Wie beim Roulette hängt auch bei der Monte-Carlo-Simulation alles von der Simulation von Zufallszahlen ab. Der Unterschied liegt jedoch darin, dass beim Roulette lediglich ein mechanischer Zufallsgenerator der Simulation zu Grunde liegt. Bei der Monte-Carlo-Simulation hingegen werden die Simulationen anhand mathematischer Algorithmen generiert. Die Zahlen wirken auch bei der Monte-Carlo-Simulation zufällig, sind aber in Wirklichkeit nur scheinzufällig, da sie von einem Algorithmus abhängig sind (Romeike & Hager, 2020, S. 380). Es wird deshalb angenommen, dass der Name Monte-Carlo von der weltbekannten Spielbank abstammt.
Ziele der Monte-Carlo-Simulation
Die Monte-Carlo-Simulation, welche ihren Ursprung in den stochastischen und statistischen Methoden hat, verfolgt das primäre Ziel der experimentellen Ermittlung von Wahrscheinlichkeitsverteilungen bei Zufallsgrössen. Dabei können, basierend auf den Risikofaktoren und deren Wahrscheinlichkeitsverteilungen, unbekannte Strukturen und Verhalten simuliert werden (Sartor & Bourauel, 2013, S. 76). Damit eine plausible und praxisnahe Einschätzung des Gesamtrisikoumfangs vorgenommen werden kann, werden bei der Monte-Carlo-Simulation mehrere zukünftig mögliche Risikoszenarien kalkuliert sowie analysiert (Gleißner, 2017, S. 254).
In der Unternehmensplanung müssen immer wieder Entscheidungen gefällt werden, welche grossen Einfluss auf die Zukunft des Unternehmens haben. Dabei müssen in der operativen Planung die Investitions-, Kosten- oder Absatzplanungen gemacht werden (Wolf, 2009, S. 545). Hierbei hängen viele verschiedene Komponenten zusammen, welche die Planung schwierig gestalten lassen. An dieser Stelle kommt die Monte-Carlo-Simulation ins Spiel. Mithilfe dieser lassen sich verschiedene Szenarien durchrechnen.
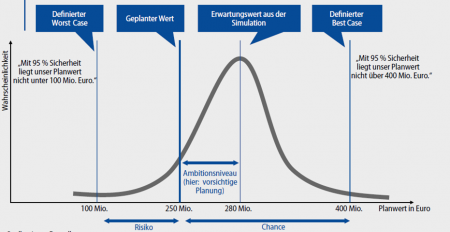
Sie ermöglicht es, für umstrittene Variablen, wie beispielsweise den Umsatz oder einzelne Kostenpositionen, unterschiedliche Planannahmen zu treffen. Schliesslich können Ergebnisse berechnet und danach in einer konsolidierten Planung zusammengeführt werden (Wolf, 2009, S. 545). Unter Berücksichtigung von Einflussfaktoren und Korrelationen wird die Entwicklung von Planpositionen (Predictive Forecasting) berechnet (Flath et al., 2015, S. 85). Die daraus entstehenden Auswertungsmöglichkeiten sind in Abbildung 1 aufgezeigt und können die Basis für Unternehmensentscheidungen bilden. Denn dadurch erhält eine Unternehmung, unter Berücksichtigung von Chancen, Gefahren und Risiken, eine konkrete Vorstellung über die Zukunft des Unternehmens (Gleißner & Wolfrum, 2019, S. 26).
Zusätzliche Einsatzmöglichkeiten sind die Berechnungen von Auswirkungen bei Veränderungen von Komponenten der Produkt- und/oder Produktionskosten oder vergleichbaren Punkten des Controllings (RiskNet GmbH, online). Ein weiteres Beispiel ist die Auswirkung eines Wechselkursrisikos, welches nicht ein Einmaliges, sondern ein dauerhaftes Risiko ist (Gleißner, 2015). Bei der Berechnung der Value at Risk Kennzahl erfreut sich die Monte-Carlo-Simulation ebenfalls grosser Beliebtheit (Bleuel, 2006, S. 372).
Vorgehensweise
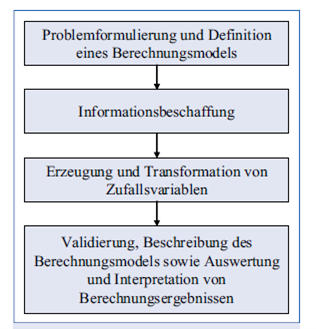
Die Durchführung einer Monte-Carlo-Simulation erfolgt in vier Schritten, welche in Abbildung 2 ersichtlich sind (Wolf, 2009, S. 547).
1. Problemformulierung und Definition eines Berechnungsmodels
Als erster Schritt soll das Problem formuliert und mittels eines mathematischen Modells abgebildet werden. Beispielsweise kann das Problem eine Illiquidität sein, welche während den nächsten 12 Monaten verhindert werden soll. Es ist dabei eine grundlegende Voraussetzung, dass die folgenden drei Bestandteile vorhanden sind respektive die Informationen dazu gesammelt werden können. Ansonsten ist eine Monte-Carlo-Simulation nicht möglich (Wolf, 2009, S. 547):
- Beeinflussbare und nicht-beeinflussbare Zufallszahlen (Beispiel: variable und fixe Kostenpositionen)
- Wirkungszusammenhänge und Abhängigkeiten dieser Zufallszahlen (Beispiel: Preis-Absatz-Funktion)
- Grundlegende Annahmen und Bedingungen (Beispiel: Weighted Average Cost of Capital (WACC))
Wesentlich ist, dass dieses Modell die Maximen «Reduzieren» und «Abstrahieren» einhält (Steinhausen, 1994, S. 21). Es sollen diejenigen Zufallszahlen ausgewählt werden, welche in der Realität tatsächlich einen wesentlichen Einfluss auf die Problemstellung haben. Mit Abstrahieren ist gemeint, dass die bestehenden Beziehungen zwischen den Zufallszahlen durch geeignete Regeln wiedergegeben werden.
2. Informationsbeschaffung
Die Quelle für den zweiten Schritt der Informationsbeschaffung bilden finanzinterne Daten wie Budgets, Jahresrechnungen und Cash-Flow-Rechnungen (Romeike, 2018, S. 178) wie auch Studien, Herstellerangaben, Expertenbefragungen und unternehmensinterne Daten (Wolf, 2009, S. 546). Einen entscheidenden Einfluss auf die realitätsgetreue Abbildung der Monte-Carlo-Simulation hat die Beurteilung der Eintrittswahrscheinlichkeit dieser Zahlen. Bei der Beschaffung der Daten wird ersichtlich, dass die Monte-Carlo-Simulation nur eine Annäherung darlegen kann. Um die Modellkomplexität gewissermassen zu reduzieren, müssen gewisse Annahmen getroffen werden.
Durch diese Annahmen wird die Komplexität des Modells verringert, gleichzeitig aber auch die vollständige und realitätsgetreue Abbildung aller Möglichkeiten eingeschränkt (Wolf, 2009, S. 547).
3. Erzeugung und Transformation von Zufallsvariablen
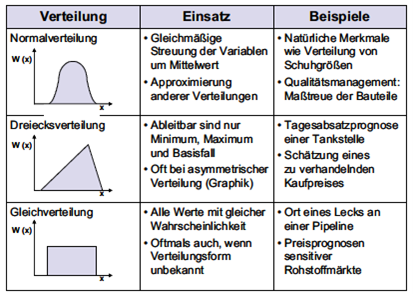
Als dritter Schritt werden die gesammelten Daten in eine Wahrscheinlichkeitsverteilung transformiert (Wolf, 2009, S. 547). Dazu muss für jede Zufallszahl ein Intervall abgrenzt werden, in welchem der Zufallswert liegen kann. Schliesslich muss die geeignete Verteilungsfunktion gewählt werden (Bleuel, 2006, S. 373). Abbildung 3 zeigt die häufigsten Verteilungsformen und deren Anwendung auf.
Diese sind wie folgt definiert (Bleuel, 2006, S. 373):
Normalverteilung: Die Normalverteilung kommt zum Einsatz bei Zufallsvariablen die gleichmässig um den Mittelwert gestreut sind, sowie zur Approximierung anderer Verteilungen. Der Bezug liegt dabei bei natürlichen Merkmalen wie beispielsweise der Verteilung von Schuhgrössen.
Dreiecksverteilung: Handelt es sich um asymmetrische Verteilungen, welche ein Minimum-, Maximum- und Basisfall darstellen, wird die Dreiecksverteilung eingesetzt. Als Beispiel dient die Tagesabsatzprognose einer Tankstelle.
Gleichverteilung: Ist die Verteilungsform nicht bekannt oder können alle Werte mit der gleichen Wahrscheinlichkeit auftreten, so wird die Gleichverteilung gewählt. Diese Form der Verteilung kommt oft bei der Preisprognose von sensitiven Rohstoffen zum Einsatz.
4. Validierung, Beschreibung, Auswertung & Interpretation
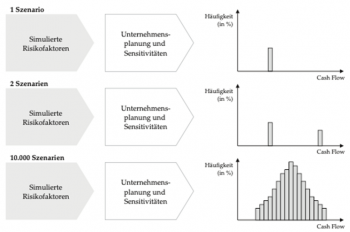
Als vierter Schritt wird die Simulation gemäss dem Gesetz der Grossen Zahl solange durchgeführt und wiederholt, bis aus den Simulationen stabile Verteilungen und Statistiken abgeleitet werden können (Möbius & Pallenberg, 2016, S. 18–20). Eine mögliche Entwicklung der Simulationsergebnisse zeigt die Abbildung 4.
Anschliessend erfolgt eine essenzielle Validierung. Ohne sie kann keine finale Auswertung und Interpretation der Ergebnisse aus den zuvor durchgeführten Berechnungen gewonnen werden. Ebenfalls soll Transparenz bezüglich der getroffenen Annahmen und des Berechnungsweges geschaffen werden. Ansonsten droht eine Ablehnung der Ergebnisse durch die Entscheidungsträger wegen fehlender Plausibilität und Transparenz (Wolf, 2009, S. 546).
Die Auswertung und Interpretation der Simulation erfolgen in mathematischen Kennzahlen und grafischen Darstellungen. Beispiele für mathematische Kennzahlen sind Mittelwerte, Standardabweichungen oder Minimum und Maximum. Besonders geeignet für die grafische Darstellung sind Histogramme, welche die Ausprägung und Häufigkeit gruppieren und so proportional aufzeigen (Wolf, 2009, S. 547).
Die getätigten Auswertungen und Interpretationen führen anschliessend im Idealfall zur Ergreifung von Massnahmen zur Risikosteuerung (Bleuel, 2006, S. 372). Computerbasierte Tools können die Rechenarbeit von Menschen übernehmen, trotzdem liegt die Validierung und Interpretation der Daten in der Verantwortung der Menschen. Dazu wird mathematisches und finanztechnisches Fachwissen benötigt (S. 376–377).
Kritische Würdigung
In diesem Abschnitt werden die Vor- und Nachteile aufgezählt und zum Schluss noch ein zusammenfassendes Fazit abgegeben.
Vorteile
- Das Vorgehen scheint nachvollziehbar und verständlich (Wolke, 2016, S. 283).
- Die Anzahl der Faktoren und unterschiedlichen Verteilungen, welche verwendet werden können, sind unbeschränkt (Wolke, 2016, S. 283).
- Es ist möglich, mehrere Einflussgrössen mit etlichen Ausprägungsmöglichkeiten zu verwenden (Wolke, 2016, S. 283).
- Die Verteilungen der Monte-Carlo-Simulation bilden die Realität besser und genauer ab als die in der Praxis gängigen Planszenarien (Wolf, 2009, S. 552).
Nachteile
- Damit die Simulation exakt ist, benötigt es eine ausreichende Anzahl an Szenarien, welche den Rechenaufwand erhöhen (Wolke, 2016, S. 284).
- Die Beziehung zwischen den generierten Zufallszahlen ist zufällig (Wolke, 2016, S. 284).
- Durch den Einsatz von unterschiedlichen Zufallsgeneratoren werden bei den verschiedenen Simulationen unterschiedliche Verteilungen der Ergebnisse und somit auch verschiedene Value at Risk erzeugt. Dadurch ist das Vergleichen der Ergebnisse nicht mehr gewährleistet. Denn der Value at Risk hängt von der verwendeten Software ab und die Genauigkeit und Transparenz sind somit nur eingeschränkt gegeben (Wolke, 2016, S. 284).
- Da oftmals keine stichfesten Daten vorliegen, müssen diese geschätzt werden. Gröbere Fehler in diesen Schätzungen führen zu Verzerrungen oder sogar falschen Ergebnissen, woraus anschliessend nicht die optimalen Rückschlüsse und Entscheidungen getroffen werden können (Romeike, 2018, S. 183).
- Die zugrundeliegenden Annahmen müssen nicht nur der Realität entsprechen, sie müssen auch nachvollziehbar sein und mit den Ansichten des Managements übereinstimmen. Ansonsten fehlt die Akzeptanz der Ergebnisse und die Simulation muss von neuem durchgeführt werden (Wolf, 2009, S. 552).
Zusammenfassung Vor- und Nachteile
Der grosse Vorteil von Monte-Carlo-Simulationen ist, dass sie als einfach anwendbare Berechnungsmethode (Romeike, 2018, S. 183), verschiedene Einzelpositionen mit unterschiedlichen Eigenschaften zu einem Gesamtbild kombiniert (Wolf, 2009, S. 552).
Trotzdem sollte sie nur dann eingesetzt werden, wenn es nicht möglich ist, eine analytische Berechnung zu machen. Denn normalerweise sind analytische Methoden in Bezug auf Vergleichbarkeit, Transparenz und insbesondere Genauigkeit deutlich besser (Wolke, 2016, S. 284, Wolf, 2009, S. 552). Monte-Carlo-Simulationen haben deshalb eher in der Forschung ihren Platz, obwohl sie auch in der Praxis einen deutlichen Zusatznutzen bringen könnten (Wolf, 2009, S. 552).
Lern- und Praxismaterialien
Quellen
Literaturverzeichnis
- Bleuel, H.-H. (2006). Monte-Carlo-Analysen im Risikomanagement mittels Software-Erweiterungen zu MS-Excel. Controlling, 18(7), 371–378.
- Diederichs, M. (2017). 3. Prozessschritte des Risikomanagements. In Risikomanagement und Risikocontrolling (4. Aufl., S. 91–181). Verlag Franz Vahlen GmbH.
- Flath, T., Biederstedt, L. & Herlitz, A. (2015). Mit Simulationen Mehrwerte schaffen. Controlling & Management Review, 59(S1), 82–89.
- Gleißner, W. (2017). 4. Risikoaggregation, Gesamtrisikoumfang und stochastische Planung. In Grundlagen des Risikomanagements: Mit fundierten Informationen zu besseren Entscheidungen (3. Aufl., S. 243–280). Verlag Franz Vahlen GmbH
- Gleißner, W. & Wolfrum, M. (2019). Risikoaggregation und Monte-Carlo-Simulation: Schlüsseltechnologie für Risikomanagement und Controlling. Springer Fachmedien Wiesbaden.
- Grisar, C. & Meyer, M. (2015). Use of Monte Carlo simulation: An empirical study of German, Austrian and Swiss controlling departments. Journal of Management Control, 26(2–3), 249–273.
- Hager, P. (2004). Corporate Risk Management: Cash Flow at Risk und Value at Risk. Bankakademie-Verl.
- Kroese, D. P. Brereton, T., Taimre, T. & Botev, Z. I. (2014). Why the Monte Carlo method is so important today. Wiley Interdisciplinary Reviews: Computational Statistics, 6(6), 386–392.
- Möbius, C. & Pallenberg, C. (2016). Risikomanagement in Versicherungsunternehmen (3. Auflage). Springer Berlin Heidelberg.
- Palisade. (ohne Datum). Was ist Monte Carlo-Simulation? - Palisade Corporation. Abgerufen am 15.03.2021 von https://www.palisade.com/risk/de/monte_carlo_simulation.asp
- RiskNet GmbH. (ohne Datum). Monte-Carlo-Simulation. Abgerufen 6. Mai 2021, von https://www.risknet.de/wissen/rm-methoden/monte-carlo-simulation/
- Romeike, F. (2018). Risikomanagement. Springer Fachmedien Wiesbaden.
- Romeike, F. & Hager, P. (2020). Erfolgsfaktor Risiko-Management 4.0. Springer Gabler.
- Sartor, F.-J. & Bourauel, C. (2013). Risikomanagement kompakt: In 7 Schritten zum aggregierten Nettorisiko des Unternehmens. Oldenbourg Verlag München.
- Steinhausen, D. (1994). Simulationstechniken. R. Oldenbourg.
- Wolf, K. (2009). Monte-Carlo-Simulation – Einsatz im Rahmen der Unternehmensplanung. Controlling, 21(10), 545–552.
- Wolke, T. (2016). Risikomanagement (3., vollständig überarbeitete, erweiterte und aktualisierte Auflage). De Gruyter Oldenbourg.
Weiterführende Literatur
- Buchhart, A. & Burger, A. (2002). Risiko-Controlling. München: Oldenbourg Wirtschaftsverlag.
- Cottin, C. & Döhler, S. (2013). Risikoanalyse: Modellierung, Beurteilung und Management von Risiken mit Praxisbeispielen. Springer Spektrum.
- Gleißner, W. & Berger, T. (2004). Auf nach Monte Carlo: Simulationsverfahren zur Risiko‐Aggregation. RISKNEWS, (1), 30–37.
- Klatt, T. Möller, K. & Pötig, S. (2010). Monte-Carlo-basierte Risikoaggregation und Risikoberichterstattung. KoR: internationale und kapitalmarktorientierte Rechnungslegung, 10 (12), 644–651.
- Metzger, D. (2008). Die Aggregation von Risiken bei der SAP AG. In Risikoaggregation in der Praxis: Beispiele und Verfahren aus dem Risikomanagement von Unternehmen (S. 51–76). Springer Berlin Heidelberg.
- Meyer-Aurich, A. (2016). Monte-Carlo-Simulation in Ökobilanzen - Chancen und Grenzen. In A. Ruckelshausen, A. Meyer-Aurich, T. Rath, G. Recke & B. Theuvsen (Hrsg.), Informatik in der Land-, Forst- und Ernährungswirtschaft 2016 (S. 125–128). Gesellschaft für Informatik.
- Papp, T. & Szoboszlai, B. (2008). Einführung einer Methodik zur Risikoaggregation bei der MOL Group. In Risikoaggregation in der Praxis: Beispiele und Verfahren aus dem Risikomanagement von Unternehmen (S. 111–129). Springer Berlin Heidelberg.
- Romeike, F. (2007). Risikomanagement in Versicherungen – Ein Überblick. Wirtschaft und Management, 4(6), 7–22.
- Winslow, M. (06.11.2018). Introduction to Monte-Carlo-Simulation in Excel 2016 [Video]. YouTube. https://www.youtube.com/watch?v=HwVBi--mE4M
- Wolf, K. (2003). Risikoaggregation anhand der Monte-Carlo-Simulation. CONTROLLING – ZEITSCHRIFT FÜR ERFOLGSORIENTIERTE UNTERNEHMENSSTEUERUNG, 15(10), 565–572.
- Wolf, K. & Runzheimer, B. (2003). Risikomanagement und KonTraG. Gabler Verlag.
Autoren
Dario Rosamina, Jonathan Schmid, Anja Strebel und Pirmin Ulrich