Holz AG – Lösung: Unterschied zwischen den Versionen
Aus Controlling-Wiki
Die Seite wurde neu angelegt: „miniatur|400px|Standardnormalverteilungstabelle (Universität Bielefeld, online) '''Berechnung z-Wert''' {| |…“ |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
[[Datei:Standardnormalverteilungstabelle.jpg|miniatur|400px|Standardnormalverteilungstabelle (Universität Bielefeld, online)]] | [[Datei:Standardnormalverteilungstabelle.jpg|miniatur|400px|Standardnormalverteilungstabelle (Universität Bielefeld, online)]] | ||
'''Berechnung z-Wert''' | ===== '''Berechnung z-Wert''' ===== | ||
{| | {| | ||
|- | |- | ||
|style="width:60px; text-align:left;" |z-Wert: || 1,6 + 0,04 = 1,64 | |style="width:60px; text-align:left;" |'''z-Wert:''' || 1,6 + 0,04 = 1,64 | ||
|- | |- | ||
| || 1,6 + 0,05 = 1,65 | | || 1,6 + 0,05 = 1,65 | ||
| Zeile 20: | Zeile 21: | ||
'''Berechnung Value at Risk (VaR)''' | ===== '''Berechnung Value at Risk (VaR)''' ===== | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
Version vom 16. Mai 2020, 17:40 Uhr
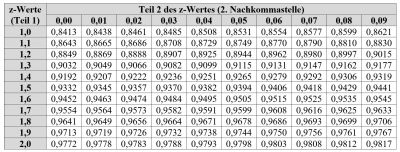
Berechnung z-Wert
| z-Wert: | 1,6 + 0,04 = 1,64 |
| 1,6 + 0,05 = 1,65 | |
| (1,64+1,65)/2 = 1,645 |
Berechnung Value at Risk (VaR)
| Firma A | Firma B: |
|---|---|
| VaR in % = μ – z * σ = 0,1 – 1,645 * 0,12 = –0,0974= –9,74% | VaR in % = μ – z * σ = 0,12 – 1,645 * 0,15 = –0,12675= –12,675% |
| VaR in Franken = " ("μ – z * σ" )" * A = (0,1 – 1,645 * 0,12) * 500’000 = –48’700 | VaR in Franken = " ("μ – z * σ" )" * A = (0,12 – 1,645 * 0,15) * 500’000 = –63’375 |
| Mit Excel: VaR in %: =NORM.INV(0.05;0.1;0.12) | Mit Excel: VaR in %: =NORM.INV(0.05;0.12;0.15) |
Dank der Berechnung des VaR wurde festgestellt, dass das Verlustrisiko der Firma A kleiner ist. Aus diesem Grund investiert die Handels AG in die Aktien der Firma A.
Aufgabe: Holz AG – Value at Risk
Grundlagen: Value at Risk
Quelle
- Universität Bielefeld (ohne Datum). Standardnormalverteilung.
