Value at Risk

Aus Controlling-Wiki

Der Value at Risk (VaR) ist eine Risiko-Masszahl, die das Verlustpotenzial eines bestimmten Szenarios quantifiziert. Sie drückt den maximalen Verlust aus, der mit einer bestimmten Wahrscheinlichkeit (etwa 95% oder 99%) innerhalb einer bestimmten Periode bzw. Haltedauer nicht überschritten wird (Wolke, 2016, S. 30). Die Kennzahl wurde Anfang der neunziger Jahre von amerikanischen Investmentbanken zur Kontrolle von Finanzmarktrisiken entwickelt. Wichtigster Grund dafür waren die Schwierigkeiten bei der Überwachung immer grösser werdender und komplexer strukturierter Portfolios (Guégan & Hassani, 2019, S. 56–57).

Grundlagen

Wie in der Einleitung bereits erwähnt wird, beschreibt der VaR die Schadenshöhe, die in einem bestimmten Zeitraum mit einer festgelegten Wahrscheinlichkeit p (Konfidenzniveau α = 1–p, meistens 95 %) nicht überschritten wird (Gleissner, 2017, S. 207).

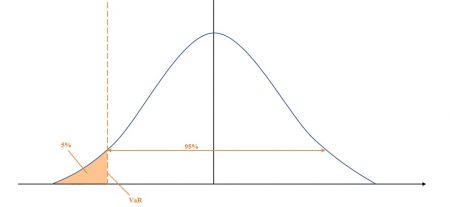
Abb. 1: Grafische Darstellung des Value at Risk (Eigene Darstellung i. A. an: Miller, 2019, S. 52)

In der Abbildung 1 wird der VaR graphisch veranschaulicht. Der berechnete VaR ist nur für das definierte Konfidenzniveau gültig. Bei einer Wahrscheinlichkeit von 5 Prozent beträgt das Konfidenzniveau 95 Prozent. Dieses besagt, welcher Verlust in 95 Prozent der Fälle nicht überschritten wird (Horsch & Schulte, 2016, S. 22).

Für die Berechnung des VaR müssen bestimmte Voraussetzungen erfüllt sein:

  • Die Risiken müssen in Einzelkategorien zerlegt und mit einer geeigneten Verteilungsfunktion beschrieben werden,
  • die Abhängigkeiten zwischen den Risiken sollten bekannt sein bzw. geschätzt werden können,
  • die Eigenschaften der Risiken müssen im Zeitablauf einigermaßen stabil und prognostizierbar sein (Extremszenarien werden nicht berücksichtigt),
  • es muss eine gesicherte Datenbasis vorhanden sein (Holtorf & Rudolf, 2000, S. 124).


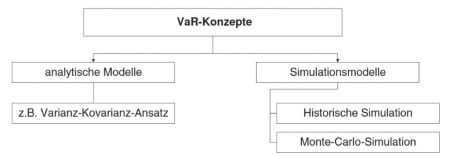
Abb. 2: Value at Risk-Konzepte im Überblick (Horsch & Schulte, 2016, S. 18)

In der Theorie gibt es verschiedene Konzepte des Value at Risk. Die Abbildung 2 zeigt drei der Ansätze und ihre Zuordnung. Es gibt analytische Modelle sowie Simulationsmodelle. Die Varianz-Kovarianz-Methode ist ein bekannter Ansatz, der zu den analytischen Modellen gehört. Die Simulationsmodelle basieren auf vergangenheitsorientierten Daten oder anderen repräsentativen Simulationen über die gleichen Risikofaktoren. Dazu gehören die historische Simulation und die Monte-Carlo-Simulation (Horsch & Schulte, 2016, S. 18).



Anwendungsmöglichkeiten

Kreditinstitute

Im Allgemeinen wird der VaR besonders im Bankenumfeld für Bewertungen herangezogen. So wird z. B. die historische Simulation oft für die Bewertung von Devisentransaktionen und -positionen verwendet (Keitsch, 2000, S. 59). Zudem dient der VaR dazu die Höhe der Mindestkapitalreserve von Kreditinstituten wie Banken festzulegen. Im internen Risikomodell berechnet sich die Höhe der Eigenkapitalreserve aus einem Sicherheitsfaktor, der mit dem durchschnittlichen VaR multipliziert wird. Die Verwendung interner Modelle ist jedoch nur für Marktpreisrisiken, nicht aber für Kreditrisiken zulässig. Deshalb macht dieses Modell nur einen Bruchteil der gesetzlichen Mindesteigenkapitalvorschriften aus (Rau-Bredow, 2001, S. 318–319).

Unternehmen

Mit dem VaR lässt sich das Gesamtrisiko einer Risikoposition oder eines Portfolios in einer leicht verständlichen Kennzahl zusammenfassen. Unternehmen können somit optimale Portfolios erstellen sowie das Risiko steuern und überwachen (Fricke, 2006, S. 1–2). Mit dem VaR können Risikopotenziale aus verschiedenen Bereichen, Portfolios oder Einzelpositionen miteinander verglichen werden. Dabei kann die Berichterstattung intern oder extern sein. Im Weiteren können auf der Basis des VaR Limit-Systeme aufgebaut werden. Der VaR dient dabei zur Festlegung der Grenzwerte, innerhalb deren Mitarbeitende ohne Rücksprache Geschäfte abschliessen dürfen. Ausserdem kann der VaR auch zur Performance-Messung eingesetzt werden. In diesem Bereich hat er das Ziel Rendite-Risiko-Relationen durch die Allokation des Risikokapitals zu optimieren (Diederichs, 2017, S. 162–163). Des Weiteren dient ein Risikomass wie der VaR zur Ermittlung des risikogerechten Eigenkapitalbedarfs (Gleissner, 2017, S. 205).

Der VaR wird grösstenteils bei Risiken, die Wertveränderungen von Vermögensgegenständen betreffen, verwendet. Für die Unternehmenssteuerung ist die Risikobewertung des operativen Geschäfts meist relevanter, weshalb alternativ in Unternehmen oft der Cashflow at Risk zur Anwendung kommt (Diederichs, 2017, S. 164–165). Mit dem Cashflow at Risk wird das gleiche Risiko wie beim VaR gemessen, er bezieht sich jedoch auf den Cashflow (Diederichs, 2012, S. 117; Gleissner, 2017, S. 207).

Berechnungsverfahren

Formel

Der VaR kann in Prozent oder als Betrag in Franken berechnet werden. Um den VaR in Prozent auszurechnen, wird von der erwartete Rendite μ der z-Wert zum dazugehörigen Konfidenzniveau subtrahiert und mit der Standardabweichung σ multipliziert. Für den VaR in Franken wird anschliessend noch mit dem Anlagewert A multipliziert (Lütolf, Rupp & Birrer, 2018, S. 626). Die einzelnen Berechnungskomponenten werden im nächsten Unterkapitel erläutert.

VaR in Prozent = μ – z * σ

VaR in Franken = (μ – z * σ )* A

μ = erwartete Rendite

σ = Standardabweichung

z = z-Wert des zugehörigen Konfidenzniveaus

A = Anlagewert


Die Berechnung kann auch mit Hilfe von Excel durchgeführt werden. Dafür wird die Wahrscheinlichkeit p, die erwartete Rendite μ sowie die Standardabweichung σ in die Excelformel norm.inv eingesetzt. Die eingefügten Werte sind als Dezimalzahlen einzutragen.

=norm.inv(p; μ; σ)

p = Wahrscheinlichkeit (1–α)

μ = erwartete Rendite

σ = Standardabweichung

Berechnungskomponenten

Zuerst wird eine Verteilung der erwarteten Rendite im gewünschten Zeitraum unterstellt. Durch diesen Schritt wird die Standardabweichung σ sowie der Erwartungswert µ ermittelt (Lütolf, Rupp & Birrer, 2018, S. 625). Zur Verfügung stehen die Varianz-Kovarianz-Methode, die historische Simulation und die Monte Carlo Simulation (Dermine, 2015, S. 308).

Methode Beschreibung
Varianz-Kovarianz-Methode Die Varianz-Kovarianz-Methode wird auch als parametrische oder analytische Methode bezeichnet. Dabei wird der VaR direkt als Funktion der Standardabweichung der Portfoliorendite bestimmt, wobei er aus den Varianzen und Kovarianzen der Marktfaktoren berechnet wird. Meistens unterliegt die Rendite einer Normalverteilung (Wolke, 2016, S. 56). Dies muss nicht immer der Fall sein, ebenso könnte beispielsweise eine t-Verteilung unterstellt werden, die eine bessere Darstellung von Ausreisser ermöglicht. Um die Berechnung durchführen zu können, müssen zunächst Varianzen und Kovarianzen der Renditen aus historischen Daten geschätzt werden. Die Vorteile der Varianz-Kovarianz sind der geringe Rechenaufwand und die Möglichkeit, eine Wenn-Dann-Analyse durchzuführen. Probleme treten auf, wenn die Rückflüsse des betrachteten Portfolios in nichtlinearer Weise von den zugrunde liegenden Risikofaktoren abhängen, was beispielsweise bei Optionen der Fall ist. Die Verteilung der Portfoliorenditen weist dann eine Schiefe auf und ist nicht mehr normalverteilt (Miller, 2019, S. 55).
Monte-Carlo-Simulation Die Monte-Carlo-Simulation ist eine umfangreiche Simulation am Computer. Dabei werden Marktpreisänderungen in vielen verschiedenen Szenarien (z. B. 10’0000 Szenarien) durchgespielt (Keitsch, 2000, S. 59). Bei dieser Methode wird die gesamte Verteilung der Wertänderung des Portfolios generiert und der VaR als entsprechendes Quantil aus dieser relativen Häufigkeitsverteilung abgeleitet. Daher kommt auch die Bezeichnung «Full Valuation Method» (Wolke, 2016, S. 60). Die Flexibilität bezüglich der Verteilungsannahmen kann als grösster Vorteil der Monte-Carlo-Simulation angesehen werden. Beispielsweise kann eine Normalverteilungen mit einer Poisson Verteilungen überlagert werden, um Extremereignisse abzubilden. Dadurch steigt der Schätzaufwand entsprechend. Nachteilig ist der hohe Rechenaufwand im Fall komplexer Portfolios zu bewerten (Miller, 2019, S. 61).
Historische Simulation Die historische Simulation ähnelt der Monte-Carlo­ Simulation. Der Unterschied ist, dass die Wertänderungen nicht mittels Zufallszahlensimulator generiert, sondern direkt aus Vergangenheitsdaten abgeleitet werden (Wolke, 2016, S. 57). Dabei wird unterstellt, dass sich die Kursentwicklung sowie die Schwankungsintensität zukünftig ähnlich verhalten werden und dadurch auf die Zukunft geschlossen werden kann (Keitsch, 2000, S. 59). Somit ist keine explizite Verteilungsannahme notwendig. Die historische Simulation ist einfach anzuwenden, wenn genügend viele Beobachtungswerte vorliegen, die als repräsentativ gelten (Wolke, 2016, S. 57).

Als nächster Schritt wird der z-Wert zum dazugehörigen Konfidenzniveau ermittelt. Bei der Annahme der Normalverteilung (gemäss Varianz-Kovarianz-Methode) kann der z-Wert aus einer Standardnormalverteilungstabelle entnommen werden.

Kritische Würdigung

Der VaR ist ein beliebtes Verfahren zur Analyse von Risikopositionen in Unternehmen, da er das Risiko in einer Kennzahl zusammenfasst. Dadurch ist sie für das Management leicht verständlich. Im Weiteren können verschiedene Teilbereiche mit einer Kennzahl verglichen werden, da es eine einheitliche Definition für alle Marktrisiken gibt. Dadurch kann eine effiziente Kapitalallokation ermöglicht werden. Ein weiterer Vorteil des Konzepts ist die Zukunftsorientierung (Fricke, 2006, S. 15–16). Diese ist jedoch nur bei den analytischen Modellen gegeben. Zudem berücksichtigt der VaR die für die Risikobeurteilung interessanten Teile der Dichte der Wahrscheinlichkeitsverteilung d. h. von minus unendlich bis zur gegebenen Zielgrösse (Gleissner, 2017, S. 208).

Der VaR besitzt einige nachteilige Aspekte. Da die Bewertung stark vereinfacht ist, wird die Realität nur noch unzureichend abgebildet (Wolke, 2016, S. 14). Die theoretische Annahme der Normalverteilung weicht in der Regel immer von den Beobachtungen in der Realität ab. Die Ursache hierfür liegt bei den zahlreichen Einflussfaktoren. So bilden sich beispielsweise Aktienrenditen nicht aufgrund einer erwarteten Normalverteilungsannahme, sondern aufgrund vielfältiger Faktoren an den Kapitalmärkten. Die Normalverteilung bei Renditen sind nur theoretische Werte, jedoch zeigt sich in der Realität bei langfristiger Betrachtung eine annähernde Normalverteilung (Diederichs, 2012, S. 164). Im Weiterem wird mit dem VaR beurteilt, mit welcher Wahrscheinlichkeit ein Verlust nicht überschritten wird. Bei dieser Analyse wird nicht ersichtlich, welche Auswirkungen das Eintreten eines grösseren Verlustes hat. Deswegen ist der Conditional Value at Risk (CVaR), auch Expected Shortfall genannt, eine immer häufiger verwendete Alternative zum VaR. Mit dem Conditional VaR wird der Erwartungswert des Eintritts eines grösseren Verlustes berechnet. Er zeigt, «welche Abweichung bei Eintritt des Extremfalls, d.h. bei Überschreitung des VaR, zu erwarten ist.» (Gleissner, 2017. S. 208–209). In jedem Fall ist neben einer VaR-Berechnung eine Szenarioanalyse zu empfehlen. In den verschiedenen Szenarien können die schlechten Entwicklungen abgebildet werden (Diggelmann, 1999, S. 185–186).

In Industrie- und Handelsunternehmen wird der VaR selten genutzt. In solchen Unternehmen ist im Vergleich zu Finanzinstitutionen ein grösserer Betrachtungshorizont interessant. Je grösser dieser Horizont wird, desto schwieriger wird es Aussagen über die Wahrscheinlichkeit zu machen sowie die dafür notwendigen Beobachtungen durchzuführen. Wie im Unterkapitel Unternehmen erwähnt ist der Cashflow at Risk dafür besser geeignet (Diederichs, 2017, S. 164–165).

Lern- und Praxismaterialien

Aufgaben

Quellen

Literaturverzeichnis

  • Dermine, J. (2015). Bank valuation & value-based management. Deposit and loan pricing, performance evaluation, and risk management (Second edition). New York: McGraw-Hill Education.
  • Diggelmann, P. B. (1999). Value at Risk. Kritische Betrachtung des Konzepts – Möglichkeiten der Übertragung auf den Nichtfinanzbereich. Zürich: Versus Verlag.
  • Holtorf, C. & Rudolf, R. (2000). Market Risk: Benchmark and Standard Model. In M. Frenkel, U. Hommel & M. Rudolf (Hrsg.). Risk Management. Challenge and Opportunity (S. 121-140). Berlin Heidelberg: Springer-Verlag.
  • Horsch, A. & Schulte, M. (2016). Wertorientierte Banksteuerung II. Risikomanagement (5. völlig überarb. Aufl.). Frankfurt am Main: Frankfurt School Verlag.
  • Keitsch, D. (2000). Risikomanagement. Stuttgart: Schäffer-Poeschel.
  • Lütolf, P., Rupp, M., & Birrer, T. K. (2018). Handbuch Finanzmanagement. Bewertungen, Finanzierungen und Risikomanagement im Rahmen der wertorientierten Unternehmensführung. Zürich: NZZ Libro.

Weiterführende Literatur

  • Hager, P. (2004). Corporate Risk Management. Cash Flow at Risk und Value at Risk. Frankfurt am Main: Bankakademie-Verlag GmbH.

Autoren

Thasana Sithamparanathan, Flamur Sulja, Céline Theiler, Benjamin Valu

Abgerufen von „https://wiki.hslu.ch/controlling/index.php?title=Value_at_Risk&oldid=14347“