Mathematische Definition der Lern- und der Erfahrungskurve

Theorie
Bruce Henderson hat für die Entwicklung des Erfahrungskurven-Konzeptes die mathematische Grundlage des Lernkurven-Konzeptes von Theodore Paul Wright übernommen. Aus diesem Grund bezieht sich die Begrifflichkeit im folgenden Beitrag auf beide Konzepte. Die beiden Konzepte lassen sich gemäss der untenstehenden Formulierung mathematisch beschreiben.
| k(X) = k1 ∙ X-b, b>0 |
Der Output k(X) beschreibt damit die Stückkosten der X-ten produzierten Einheit in Abhängigkeit vom Input X. Der Input X zeigt die kumulierte Menge der produzierten Einheiten. k1 reflektiert die Stückkosten der ersten hergestellten Einheit und der Parameter b steht für den Lernkoeffizient. Dieser lässt sich mithilfe der nachstehenden Formel definieren.
| b = [math]\displaystyle{ \frac{-log (v)}{log (2)} }[/math] |
v steht dabei für die Lernkurve. Gemäss Henderson sinken die Produktionskosten bei jeder Verdoppelung der kumulierten Menge der produzierten Einheiten um 20-30%. Für die Berechnung der Lernkurve kann also dieser Rückgang der Produktionskosten der Zahl eins subtrahiert werden. Folglich resultiert eine Lernkurve von 70-80 % (Sabel & Weiser, 2008, S. 53-54).
Zahlenbeispiel
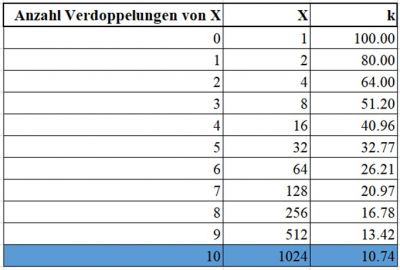
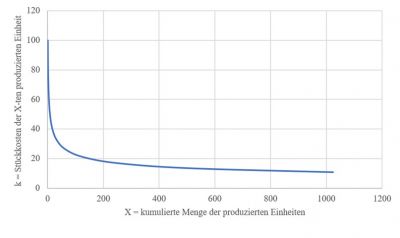
Die geschilderte Theorie wird in Abbildung 1 und 2 an einem Zahlenbeispiel veranschaulicht. k1 = 100 und eine Lernkurve von 80% seien gegeben. Die erste Spalte in Abbildung 1 widerspiegelt die Anzahl der erfolgten Verdoppelungen von X. Die zweite Spalte zeigt die Zeitpunkte, an denen sich X verdoppelt und die dritte Spalte zeigt die entsprechende Veränderung von k. In der Abbildung 2 werden die Werte der Abbildung 1 visualisiert (Sabel & Weiser, 2008, S. 53-54).
Die Berechnung anhand der Funktion k(X) wird untenstehend aufgeführt. Die Aufgabenstellung sei die gleiche. In Abbildung 1 sind die zu berechnenden Werte blau hinterlegt.
| b = [math]\displaystyle{ \frac{-log (v)}{log (2)} }[/math] = [math]\displaystyle{ \frac{-log (0.8)}{log (2)} }[/math] = 0.32 |
| k(X) = k1 ∙ X-b = 100 ∙ 1024-0.32 = 10.74 |
Wird also die kumulierte Menge der produzierten Einheiten zehnmal verdoppelt, so können die Kosten gemäss der Theorie von 100 auf 10.74 pro Stück sinken. Ist in einer Fragestellung die Lernkurve nicht gegeben, muss die Funktion k(X) durch Logarithmieren in eine lineare Funktion umgeformt werden. Notwendig ist eine solche Berechnung beispielsweise, wenn die Effekte des Erfahrungskurven-Konzeptes im Rahmen der empirischen Forschung beobachtet und bestimmt werden sollen. Auf diese Vorgehensweise wird im vorliegenden Beitrag aber nicht weiter eingegangen (Sabel & Weiser, 2008, S. 53-54).
Interpretation
Die Interpretation der berechneten Werte ist jedoch vorsichtig anzustellen. Zum einen bildet die Funktion, wie in Abbildung 2 zu erkennen ist, eine horizontale Asymptote, was ökonomisch unlogisch ist. Es liegt auf der Hand, dass nach einer gewissen Anzahl Verdoppelungen von X, wie sie in Abbildung 1 in der ersten Spalte aufgeführt sind, sich k, beziehungsweise die dritte Spalte in Abbildung 1, nicht weiter reduzieren kann. Im Verlaufe der Zeit sind die Effekte des Erfahrungskurven-Konzeptes also gewissermassen ausgeschöpft (Sabel & Weiser, 2008, S. 55).
Zum anderen werden in der mathematischen Definition auch keine Anfangserfahrungen berücksichtigt, obwohl die absoluten Kostenersparnisse bei den ersten zehn Einheiten mit Abstand am stärksten sind. Um diesen Problemstellungen für die Anwendung der Funktion Rechnung zu tragen, wurden weitere Modifikationen der Formel entwickelt. Auf diese wird im vorliegenden Eintrag jedoch nicht eingegangen (Sabel & Weiser, 2008, S. 55).
Grundsätzlich kann festgehalten werden, dass durch eine individuelle Festlegung eines sinnvollen Definitionsbereiches die vorher beschriebenen Problemfelder eingegrenzt werden können. Dies erweist sich in der Praxis jedoch als ebenso schwierig wie aufwändig (Sabel & Weiser, 2008, S. 55).
Quellen
- Sabel, H. & Weiser, Ch. (2008). Dynamik im Marketing. Umfeld – Strategie – Struktur – Kultur (4. Auflage). Wiesbaden: Gabler.
Autoren
Nicolas Ammann, Fabian Arnold, Raphael Bucheli
