Quantitative Methoden: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (9 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Geprueft|+}} | |||
Quantitative Prognosemethoden können nebst den [[Qualitative Methoden|qualitativen Methoden]] als Instrumente für Planungen angewendet werden. Hierbei wird mithilfe von Daten oder auch [[Big Data]] vergangenheitsbasierte Daten ausgewertet und für zukünftige Perioden abgeleitet. Diese Methoden kommen bei der [[Planung und Budgetierung]] für beispielsweise den [[Absatzplan]] oder den [[Finanzplan]] zur Anwendung. | |||
== Gleitender Durchschnitt == | |||
[[Datei:Berechnung gleitender Durchschnitt.png|300px|mini|Abbildung 1: Berechnung gleitender Durchschnitt (in Anlehnung an Lütke Entrup & Goetjes, 2019, S. 74)]] | |||
Anhand des gleitenden Durchschnitts kann die zukünftige Menge prophezeit werden. Für die Berechnung werden beispielsweise die Absätze von diversen vergangenen Monaten berücksichtigt. | |||
In der Grafik ist ein Beispiel für einen dreimonatigen oder fünfmonatigen gleitenden Durchschnitt aufgezeigt. Beim dreimonatigen gleitenden Durchschnitt werden für die Planmenge der Durchschnitt von drei IST-Mengen berücksichtigt. Je grösser das Zeitintervall ist, desto mehr werden Schwankungen in den Erfahrungswerten geglättet (Lütke Entrup & Goetjes, 2019, S. 73–75). | |||
| Zeile 15: | Zeile 16: | ||
Der gleitende Durchschnitt | == Gewichteter gleitender Durchschnitt == | ||
Der gleitende Durchschnitt kann vor allem dann verwendet werden, wenn die Mengen wenige bis keine saisonalen Schwankungen aufweisen und die Planwerte somit über das gesamte Jahr voraussichtlich stabil bleiben. Werden saisonale Schwankungen angenommen, können die IST-Mengen in den einzelnen Monaten unterschiedlich gewichtet werden. Hierbei wird von einem gewichteten gleitenden Durchschnitt gesprochen (Lütke Entrup & Goetjes, 2019, S. 73–75). | |||
Der gleitende Durchschnitt wie auch der gewichtete gleitende Durchschnitt eignen sich für einfache Forecastings und bedarf keinen speziellen Softwares. Sie sind vor allem für Unternehmen empfehlenswert, welchen es an Ressourcen einer fundierten Vergangenheitsanalyse fehlt oder eine tiefgründige Analyse nicht als nötig erachten. | |||
= | == ARIMA Modell == | ||
Das ARIMA Modell (Autoregressive integrated moving avarage) eignet sich, um stationäre vergangenheitsbasierte Zeitreihen analysieren zu können, um so mathematische Prognosen für zukünftige Planungen herzuleiten (Lütke Entrup & Goetjes, 2019, S. 78). Die Verwendung des ARIMA-Models bedarf ein fundiertes Wissen von Statistik und benötigt somit auch geeignetes Personal oder externer Beratung. | |||
== Regressionsanalyse == | |||
Mithilfe der Regressionsanalyse kann die Planung anhand einer mathematischen Funktion geplant werden. Die Analyse berechnet die Beziehung zwischen einer oder mehreren unabhängigen Variablen und einer oder mehreren abhängigen Variablen. Je nach Anzahl von abhängigen oder unabhängigen Variablen wird von einer anderen Klassifizierung der Regressionsanalyse gesprochen. Als Beispiel dient die multiple Regressionsanalyse. Sie zeigt die Beziehung zwischen mindestens zwei unabhängigen und einer abhängigen Variablen (Bas, 2020, 296–297). Diese Art der Regressionsanalyse kann für folgende Fragestellungen herangezogen werden (Kuhne, 2015, S. 4): | |||
* Wie verhält sich die Menge (abhängige Variable), wenn sich der Preis (erste unabhängige Variable) erhöht oder gesenkt wird und die Marketingausgaben (zweite unabhängige Variable) erhöht oder gesenkt werden? | |||
* | * Welche unabhängige Variable hat den grössten Einfluss auf die Planung? | ||
* | |||
=Autoren= | == Lern- und Praxismaterialien == | ||
{| class="wikitable" | |||
|- | |||
! Aufgaben | |||
|- | |||
| [[Quantitative Methoden - Verständnisfragen & Quiz ]] | |||
|} | |||
== Quellen == | |||
* Bas, E. (2020). [https://doi.org/10.1007/978-3-658-32120-8_7 Regressionsanalyse]. In E. Bas (Hrsg.), Einführung in Wahrscheinlichkeitsrechnung, Statistik und Stochastische Prozesse (S. 296–314). Springer Fachmedien Wiesbaden. | |||
* Kuhne, D. (2015). [https://link.springer.com/chapter/10.1007/978-3-658-04492-3_1 Multiple Regression als Konzept zur Absatzprognose]. In O. Gansser & B. Krol (Hrsg.), Markt- und Absatzprognosen: Modelle—Methoden—Anwendung (S. 27–48). Springer Fachmedien Wiesbaden. | |||
* Lütke Entrup, M., & Goetjes, D. (2019). [https://doi.org/10.1007/978-3-658-22891-0_3 Sales & Operations Planning-Prozess]. In M. Lütke Entrup & D. Goetjes (Hrsg.), Sales & Operations Planning in der Konsumgüterindustrie: Mit Best-Practice-Prozessen nachhaltig die Wettbewerbsfähigkeit steigern (S. 9–53). Springer Fachmedien Wiesbaden. | |||
* Lütke Entrup, M., & Goetjes, D. (2019). [https://doi.org/10.1007/978-3-658-22891-0_4 Systemgestützte Absatzplanung]. In M. Lütke Entrup & D. Goetjes (Hrsg.), Sales & Operations Planning in der Konsumgüterindustrie: Mit Best-Practice-Prozessen nachhaltig die Wettbewerbsfähigkeit steigern (S. 55–104). Springer Fachmedien Wiesbaden. | |||
== Autoren == | |||
Yvonne Birrer, Nicole Furrer, Fabienne Kretschmar, Endrit Muçaj | Yvonne Birrer, Nicole Furrer, Fabienne Kretschmar, Endrit Muçaj | ||
Aktuelle Version vom 3. Oktober 2022, 08:18 Uhr

Quantitative Prognosemethoden können nebst den qualitativen Methoden als Instrumente für Planungen angewendet werden. Hierbei wird mithilfe von Daten oder auch Big Data vergangenheitsbasierte Daten ausgewertet und für zukünftige Perioden abgeleitet. Diese Methoden kommen bei der Planung und Budgetierung für beispielsweise den Absatzplan oder den Finanzplan zur Anwendung.
Gleitender Durchschnitt
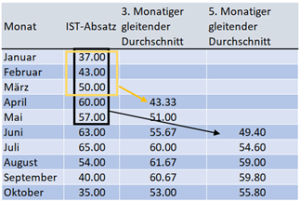
Anhand des gleitenden Durchschnitts kann die zukünftige Menge prophezeit werden. Für die Berechnung werden beispielsweise die Absätze von diversen vergangenen Monaten berücksichtigt.
In der Grafik ist ein Beispiel für einen dreimonatigen oder fünfmonatigen gleitenden Durchschnitt aufgezeigt. Beim dreimonatigen gleitenden Durchschnitt werden für die Planmenge der Durchschnitt von drei IST-Mengen berücksichtigt. Je grösser das Zeitintervall ist, desto mehr werden Schwankungen in den Erfahrungswerten geglättet (Lütke Entrup & Goetjes, 2019, S. 73–75).
Gewichteter gleitender Durchschnitt
Der gleitende Durchschnitt kann vor allem dann verwendet werden, wenn die Mengen wenige bis keine saisonalen Schwankungen aufweisen und die Planwerte somit über das gesamte Jahr voraussichtlich stabil bleiben. Werden saisonale Schwankungen angenommen, können die IST-Mengen in den einzelnen Monaten unterschiedlich gewichtet werden. Hierbei wird von einem gewichteten gleitenden Durchschnitt gesprochen (Lütke Entrup & Goetjes, 2019, S. 73–75).
Der gleitende Durchschnitt wie auch der gewichtete gleitende Durchschnitt eignen sich für einfache Forecastings und bedarf keinen speziellen Softwares. Sie sind vor allem für Unternehmen empfehlenswert, welchen es an Ressourcen einer fundierten Vergangenheitsanalyse fehlt oder eine tiefgründige Analyse nicht als nötig erachten.
ARIMA Modell
Das ARIMA Modell (Autoregressive integrated moving avarage) eignet sich, um stationäre vergangenheitsbasierte Zeitreihen analysieren zu können, um so mathematische Prognosen für zukünftige Planungen herzuleiten (Lütke Entrup & Goetjes, 2019, S. 78). Die Verwendung des ARIMA-Models bedarf ein fundiertes Wissen von Statistik und benötigt somit auch geeignetes Personal oder externer Beratung.
Regressionsanalyse
Mithilfe der Regressionsanalyse kann die Planung anhand einer mathematischen Funktion geplant werden. Die Analyse berechnet die Beziehung zwischen einer oder mehreren unabhängigen Variablen und einer oder mehreren abhängigen Variablen. Je nach Anzahl von abhängigen oder unabhängigen Variablen wird von einer anderen Klassifizierung der Regressionsanalyse gesprochen. Als Beispiel dient die multiple Regressionsanalyse. Sie zeigt die Beziehung zwischen mindestens zwei unabhängigen und einer abhängigen Variablen (Bas, 2020, 296–297). Diese Art der Regressionsanalyse kann für folgende Fragestellungen herangezogen werden (Kuhne, 2015, S. 4):
- Wie verhält sich die Menge (abhängige Variable), wenn sich der Preis (erste unabhängige Variable) erhöht oder gesenkt wird und die Marketingausgaben (zweite unabhängige Variable) erhöht oder gesenkt werden?
- Welche unabhängige Variable hat den grössten Einfluss auf die Planung?
Lern- und Praxismaterialien
| Aufgaben |
|---|
| Quantitative Methoden - Verständnisfragen & Quiz |
Quellen
- Bas, E. (2020). Regressionsanalyse. In E. Bas (Hrsg.), Einführung in Wahrscheinlichkeitsrechnung, Statistik und Stochastische Prozesse (S. 296–314). Springer Fachmedien Wiesbaden.
- Kuhne, D. (2015). Multiple Regression als Konzept zur Absatzprognose. In O. Gansser & B. Krol (Hrsg.), Markt- und Absatzprognosen: Modelle—Methoden—Anwendung (S. 27–48). Springer Fachmedien Wiesbaden.
- Lütke Entrup, M., & Goetjes, D. (2019). Sales & Operations Planning-Prozess. In M. Lütke Entrup & D. Goetjes (Hrsg.), Sales & Operations Planning in der Konsumgüterindustrie: Mit Best-Practice-Prozessen nachhaltig die Wettbewerbsfähigkeit steigern (S. 9–53). Springer Fachmedien Wiesbaden.
- Lütke Entrup, M., & Goetjes, D. (2019). Systemgestützte Absatzplanung. In M. Lütke Entrup & D. Goetjes (Hrsg.), Sales & Operations Planning in der Konsumgüterindustrie: Mit Best-Practice-Prozessen nachhaltig die Wettbewerbsfähigkeit steigern (S. 55–104). Springer Fachmedien Wiesbaden.
Autoren
Yvonne Birrer, Nicole Furrer, Fabienne Kretschmar, Endrit Muçaj
